Pensemos en una modificación del enunciado:
|
Se requiere un algoritmo que nos muestre de todas las ventas mensuales de un determinado año, cuales meses estuvieron por debajo del promedio de venta mensual ordenados primero el de menor venta luego el que le sigue y así sucesivamente. |
En otras palabras, queremos saber los que están por debajo del promedio, pero queremos verlos ordenados desde el menor al mayor.
Volvamos a plantear el método top-down:
- Carga de los 12 totales de ventas y Cálculo del
- Ordenamiento del
- Muestra de las ventas de menor a mayor hasta que encontremos una que supere el
Vemos que el primer punto se mantiene tal cual, así que tenemos una gran parte hecha, concentrémonos ahora en el ordenamiento ¿Cómo se ordena un vector?
Existen varios algoritmos diseñados para ordenamiento de vectores, cada uno con sus ventajas y desventajas. La idea es poder entenderlos y aplicarlos al algoritmo actual. Vamos a elegir uno simple de entender: el método de ordenamiento de comparaciones sucesivas.
Veamos el diagrama de flujo de este método de ordenamiento:
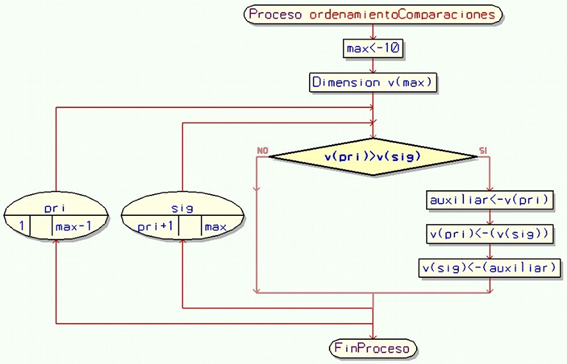
En este método se utiliza el mecanismo de buscar el menor y ponerlo al principio. Para hacer esto se toma el primer elemento del vector (v[pri]) y se lo va comparando con todos los restantes (v[sig]), cada vez que encontremos uno que sea menor lo intercambiaremos con la primera posición. Al finalizar de comparar el primer elemento con todos los siguientes estaremos seguros de que el menor quedó en la primera posición. Lo siguiente será repetir la misma búsqueda del menor ahora a partir de la segunda posición y los restantes, luego con la tercera y así hasta la anteúltima, por descarte en la última posición quedará el mayor.

Este método es bastante simple de entender, pero lamentablemente es de muy baja performance (rendimiento) ya que requiere que se comparen los elementos del vector todos con todos por lo tanto al crecer en una unidad el vector se suma un ciclo entero de comparaciones.
|
Elementos del vector |
Cantidad de comparaciones |
|
2 |
1 |
|
3 |
3 ( 1 + 2 ) |
|
4 |
6 ( 3 + 3 ) |
|
5 |
10 ( 6 + 4 ) |
|
6 |
15 ( 10 + 5 ) |
|
7 |
21 (15 + 6 ) |
|
8 |
28 ( 21 + 7 ) |
|
9 |
36 ( 28 + 8 ) |
|
10 |
45 ( 36 + 9 ) |
Lo invito a prestar atención a esta progresión pues más adelante buscaremos un método para calcularla.
Apliquemos entonces este método de ordenamiento al algoritmo. Pues bien, nos encontramos con un problema, he aquí que el mes de las ventas está asociado al índice así que tendremos que guardar el mes en un vector auxiliar e intercambiarlo a medida que cambiamos las ventas así no perdemos la relación. Vamos a tener que rehacer todo el Algoritmo:

y el diagrama de flujo :
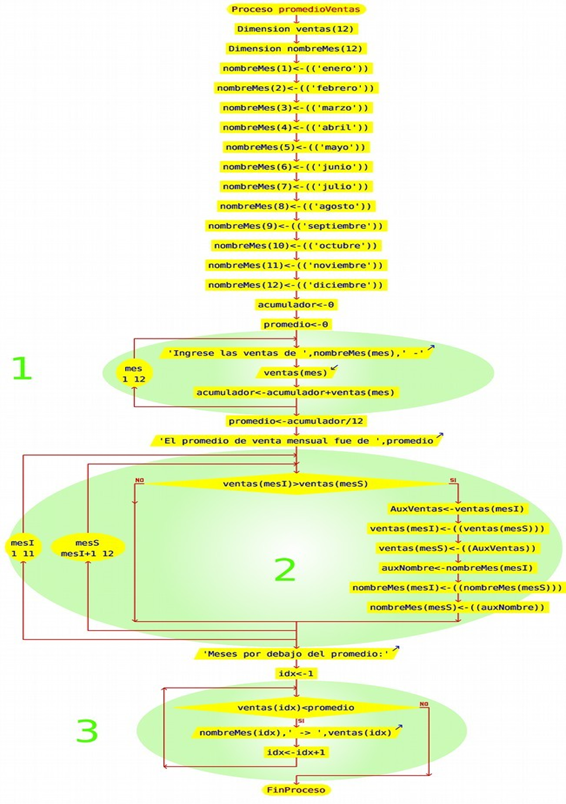
Analicemos el diagrama, primero tenemos la declaración de las variables y la definición del vector con los nombres de los meses. A continuación, tenemos 3 ciclos importantes, veámoslo uno por uno:
El ciclo 1 corresponde a la carga del vector de ventas y al cálculo del promedio, tal cual como lo hemos visto anteriormente, el único cambio es en el mensaje: en lugar de mostrar el número de cada mes, aprovechamos y mostramos su nombre.
El ciclo 2 corresponde al ordenamiento tanto del vector de ventas de mayor a menor como también del vector de nombres (nombreMes) que debe mantener la asociación con el mes de la venta.
El ciclo 3 ahora es una estructura repetitiva condicional, en lugar de una iteración aprovechamos que el vector está ordenado y mientras las ventas sean menores al promedio se mostrarán los datos del vector, apenas superemos el promedio ya no se deberá mostrar nada más.
Si usted quiere como tarea adicional podría agregar a continuación otro ciclo para que muestre las ventas ordenadas que superan al promedio, no olvide poner el título “Meses por arriba del promedio” para evitar confusiones en los datos.
Pero, ¿Hay algún método de ordenamiento mejor y que sea fácil de entender?