Sigamos pensando sobre el mismo algoritmo.
En el caso que el usuario se equivoque, entonces, ¿deberá ejecutar nuevamente el algoritmo desde cero? Por ahora la respuesta es: Sí, deberá comenzar de nuevo con el algoritmo. ¿Y qué pasa si quiero conocer el perímetro y la superficie de varios triángulos? ¿No habrá una forma de que me siga permitiendo calcular las veces que yo quiero sin tener que ejecutar nuevamente el algoritmo? O mejor... No se podrá modificar el algoritmo para que me indique cual es el triángulo de mayor área de un grupo de triángulos que quiero procesar? Bueno.. ya es pedir mucho... reformulemos primero el enunciado del problema.
|
Calcular el área y el perímetro de varios triángulos conociendo el largo de los 3 lados y determinar cuál de ellos tiene el área mayor. |
En primer lugar, evaluemos que significa calcular “varios” triángulos, eso implica que debemos repetir el cálculo una y otra vez a medida que se ingresan los 3 lados. Para esto utilizaremos la estructura repetitiva que en pseudocódigo se escribe cómo:
|
Mientras <expresión_logica> Hacer <bloque de instrucciones> Fin Mientras |
La expresión lógica es la que determina si se volverá a ejecutar el bloque de instrucciones mientras sea de resultado verdadero, cuando la expresión tiene como resultado falso entonces ya no se ejecutará más el bloque y se seguirá con la secuencia normal.
Pero para encarar el nuevo algoritmo debemos agregar a las incógnitas conocidas y analizadas, una nueva variable que será el mayor valor de área calculado. Esta variable no se resuelve en forma directa como el área y el perímetro. Si tuviéramos que resolver el problema de la mayor área con lápiz y papel seguramente haríamos todos los cálculos de todas las áreas y luego al finalizar revisaríamos todo para encontrar el mayor, el problema es que el algoritmo diseñado no recuerda los valores ingresados, tan sólo el último procesado. Pero hay un método mejor para aplicarlo al modo de cálculo de la computadora según conocemos hasta el momento. Esta forma requeriría que cada vez que hagamos un cálculo comparemos si el área es la mayor encontrada hasta ese momento, en este caso cuando lleguemos al final estaremos seguros que hemos comparado cada área a medida que la calculábamos. Además, será mejor que guardemos cuales eran los lados ingresados para recordarle al usuario al finalizar el proceso.
El otro tema que falta resolver es darnos cuenta cuando no hay más triángulos que procesar, una forma sería preguntar al usuario si hay más triángulos, cuando él diga que no entonces se dejará de calcular y se podrá mostrar el mayor.
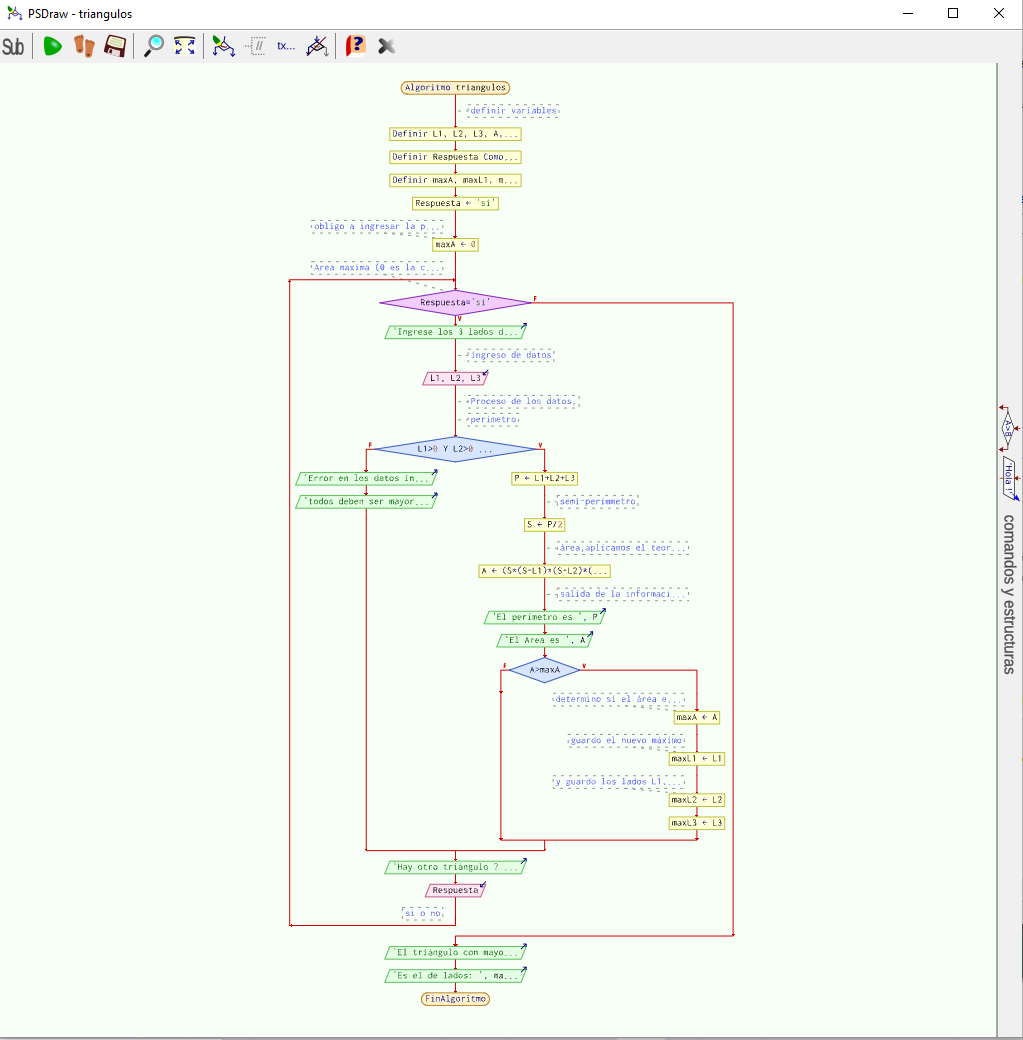
Entonces el algoritmo en pseudocódigo quedaría de la siguiente forma:
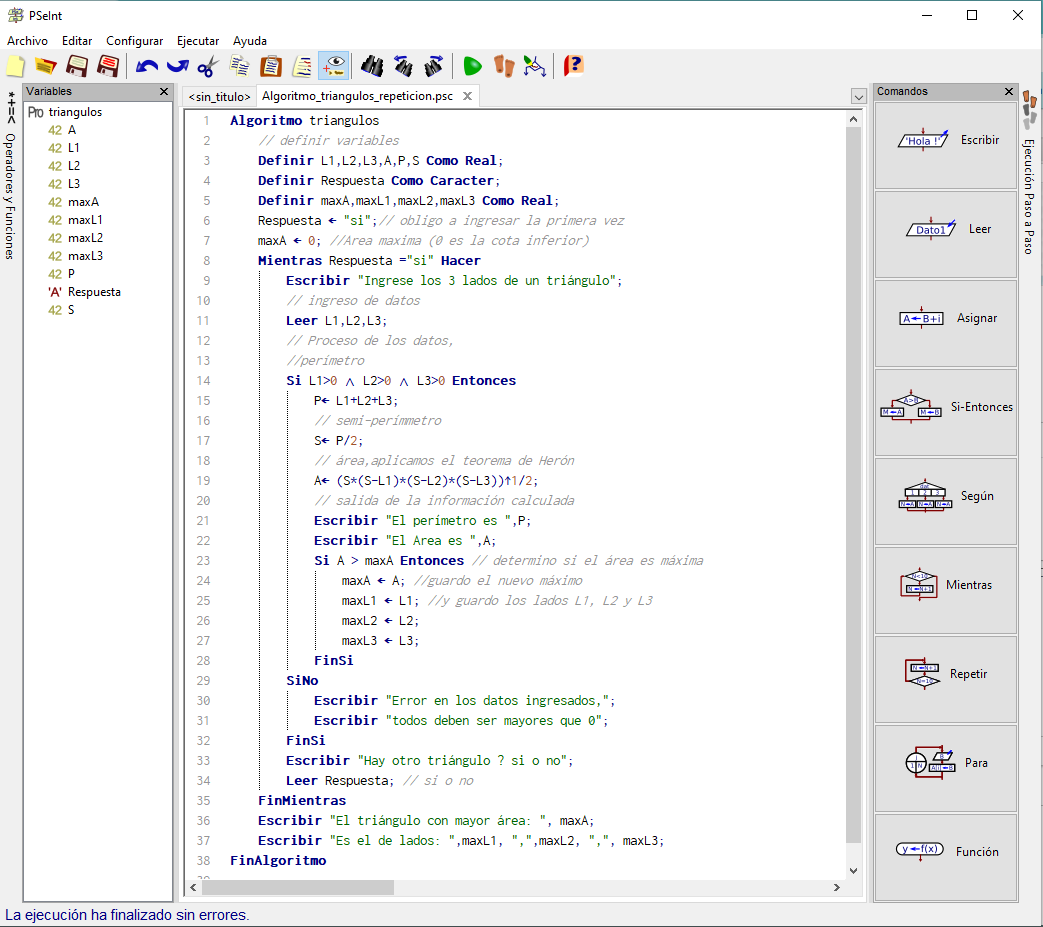
y su respectivo diagrama: